首先请大家看一个 非常有趣 的恶作剧。

然后,本文就结束了。

我们每个人都有过被恶作剧恶搞的经历(如果没有,那现在就有了)。我们不禁要问, 为 什么总会有恶作剧发生?为什么我们总会被成功恶搞?我们究竟该怎么避免恶作剧? 小朋友,请收起你的问号,让我们来理性地分析分析。

恶作剧可能会迟到,但从不缺席
假设张三和李四是好朋友,到了愚人节这一天,他们要 选择是否恶搞对方 。这是一个策略抉择的问题,按照博弈论中常用的思路,我们首先需要考虑他们的 收益矩阵 。
如果 两个人 都选择 不恶搞 ,一起喝茶聊天,那他们一定会觉得这样很不错,所以假定此时两个人的满意度收益都是 2 。
如果两人中, 只有一个人选择恶搞 ,那么没有选择恶搞的那个人一定因为被人恶搞而很气,所以假设被恶搞的人的满意度收益为 -1 。而搞恶作剧的人因为看到自己的恶作剧成功,满意度爆棚,所以假设他的满意度收益为 5 。

如果 两个人都选择恶搞 ,那么两个人虽然恶搞了别人,但是自己也被别人恶搞了,二者相抵消,所以两个人满意度收益都是 0 。由此我们可以列出两人 单次博弈 的收益矩阵:

假设两个人都选择使用 纯策略 进行博弈。如下图, 纵着看收益矩阵 ,可以看出,无论李四是否选择恶搞,张三都会选择恶搞以获得更高的满意度。而对于李四,他知道张三一定会选择恶搞,所以他抱着“ 我宁愿小亏也不让你血赚 ”的心态,也选择了恶搞。这样双方就达到一个 纳什均衡 。
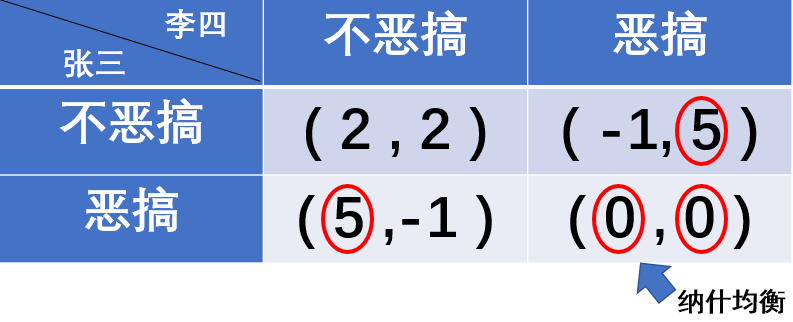
所谓纳什均衡,就是指 博弈双方处于非常焦灼的状态 ,都 不愿意在当前的决策上做出改变 。从这一模型中,我们可以知道, 搞恶作剧其实是挺合理的一件事 。
上面的模型只是考虑了单次博弈的情况,实际情况中,张三和李四每年愚人节都要进行这样的博弈。但是,经过几次博弈以后,张三和李四发现,他们 都不恶搞的收益其实是比都恶搞的收益高 的(从收益矩阵中可以看出),所以他们进行了一次协商, 相互承诺下次一定不恶搞 了。

但是,李四知道,张三是出了名的无赖,他经常不信守承诺,所以,为了避免张三违约,让自己吃亏,李四决定采用“ 恐怖扣扳机 ”策略,即李四一直保持信守承诺,不搞恶作剧,一旦张三出现一次违约行为,那在接下来的博弈中,李四就会撕破脸皮,开始恶搞。

作为李四的朋友,张三觉得 没有人比他更懂李四 ,他也料到李四会采取“ 恐怖扣扳机 ”策略来防范自己违约,所以,他需要对自己采取的策略进行权衡。
与前一个博弈不同,这是一个 重复博弈 。且结合实际,我们假设张三和李四每过一年都有一定的概率P出现“ 友尽 ”的情况,这里“友尽”的含义是指双方再也不联系,成为最遥远的朋友(想想以前的发小,这样假设还挺真实)。

如果张三选择了违约继续恶作剧,那么他今年可以直接获得收益 5 ,但在以后的博弈中,李四“扣动扳机”,开始恶搞,张三被迫也得选择恶搞,因此以后获得的收益全都是 0 ,所以 违约给张三带来的总收益期望为5 。

如果张三选择一直信守承诺,那么今年他将获得收益 2 ,由于他在第二年 有(1-P)的概率和李四做朋友 ,所以获得的收益期望为 2(1-P) ,第三年还和李四做朋友的概率为 ( 1-P ) 2 ,获得的收益期望为 2( 1-P ) 2 ,依次类推,第n年获得的收益期望为2(1-P) n-1 。用 等比数列求和公式 ,将无穷多项期望求和可以得出,信守承诺给张三带来的总收益期望为 2/P 。

这样一来,张三就可以得出“ 违约的诱惑 ”有多大。即,当张三和李四“友尽”的概率小于40%时, 2/P 大于 5 ,信守承诺的收益要比违约的高。当张三和李四“友尽”的概率大于40%时, 2/P 小于 5 ,违约搞恶作剧会有更高的收益。这告诉我们, 张三是否违约取决于他和李四“友尽”的概率 。
实际上,随着时间的推移,张三和李四“友尽”的概率会越来越高,最终,张三一定会不装了,他摊牌了,他是无赖。所以,他最后一定会违约,选择对李四进行恶作剧,使博弈来到纳什均衡点。这就解释了 为什么恶作剧迟早是会发生的 。

根据上面的分析,我们也明白了 为什么临近毕业,你和你的同学会开始放飞自我,各种整蛊恶搞。为什么散伙饭往往会吃得很嗨。 为什么经常会出现“烂尾”的情况。
毕竟: 恶作剧可能会迟到,但从不缺席 。
你以为你以为的就是你以为的吗
恶作剧之所以能成功捉弄人,很大一部分原因是我们 对事物的辨别 出现了偏差,就像下图,路人以为橱窗中所放置的是模型,但其实是人假扮的。

要弄清为什么人会在辨别事物时产生误差,就需要我们先理清人在辨别事物时的流程。

假设你的面前出现了一只哈士奇。首先,人眼会自动获取哈士奇的图像。在获取的过程中,由于人眼的自身特性,比如:只有 一定波长范围内的光可见 , 视觉暂留 等,使得所获得的图像被预处理。然后,图像被送到大脑,大脑根据自己的经验记忆进行对照,从而识别出图像中的特征,比如, 中二的表情 , 厚厚的毛发 。最后,大脑根据所提取的所有特征,对图片中的事物进行分类,得出结论:这是一只哈士奇。
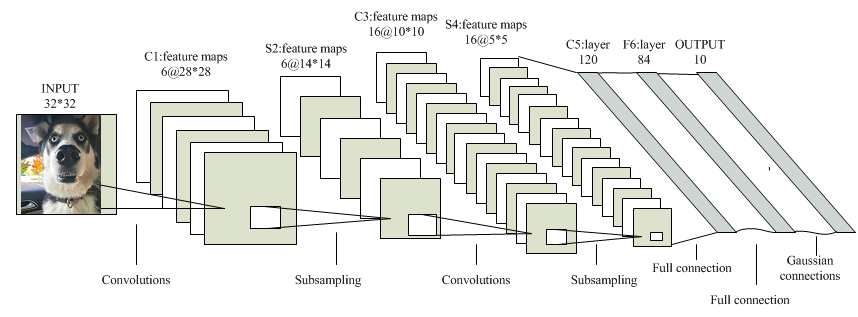
识别流程示意图(CNN)
我们使用这一模型,逐条分析是哪些因素导致我们对事物的辨别出现了问题。
首先,人眼 获取 图像 ,这一点很trivial(平凡),它的影响基本可以排除(星际玩家除外)。

其次,人眼自身的特性带来的 预处理 。由于我们通常遇到的事物不会引发我们的各种视觉效应,所以,它的影响我们也不做考虑。

静止还是运动?
然后是 特征提取 ,模型中指出,特征提取所需要的是人的经验与记忆,这是一个 长期接触训练 的结果。通俗来讲就是, 只是因为在人群中瞅了你一眼 , 大概率会忘掉你容颜 。 如果在人群中多瞅你几眼 , 就再也没能忘掉你容颜 。

通过一次又一次的识别训练,我们就能对事物的特征有更加深刻的印象,从而在下一次遇见时,准确将它识别出来。这就告诉我们, 如果你被恶作剧的次数不够多 , 那么你就很难识别出一个恶作剧 。

最后是 分类 ,这一步就相当于,我们 根据一个人脑袋大脖子粗 , 推断他不是大款就是伙夫 。这里存在一个这样的问题, 我们只会将事物归类到我们已知的事物类型中 ,如果这个事物对你来说是船新的,那么我们的判断就会出现错误。

比如说,你看到一个人身着女装,你会根据常识,自然而然地以为这个人是个女生。但是,他也有可能是位女装大佬,只不过你可能之前没有接触过女装大佬,大脑中 没有储存这样的类别标签 ,所以大脑不会输出这样的结果。这告诉我们, 如果你没有被恶作剧过 , 那你识别出恶作剧的概率几乎为0 。

所以说,眼见不为实, 你以为你以为的就是你以为的 (请写出每个“以为”的含义),实际上, 你以为的反而是你不以为的 。
物理虽头秃但有用
通过前面的分析我们知道,恶作剧是必然会出现的,而且恶作剧是很难被识破的。所以, 既然恶搞防不住 ,为何 我们 不加入?因此,我们选择献上物理知识,加入恶搞军团。

阿伟就是其中的一位,他一直想用恶作剧吓一吓杰哥,好让杰哥不敢再欺负他。于是他约杰哥到一座山上,说要分享一些好康的东西。
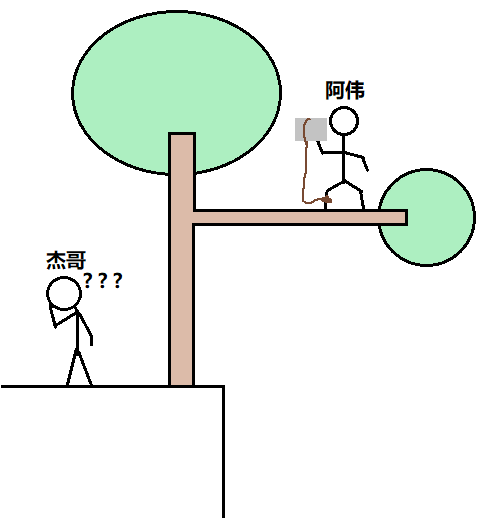
当时的情形是这样的
杰哥应邀来到山顶,却只见到阿伟站在悬崖边的一棵树的树枝上, 脚上绑了一根绳子 , 绳子的另一端绑着一块石头 ,拿在手上。杰哥感到十分奇怪,问到:到底有什么东西, 让我康康 。

阿伟啥也没说,先是 将手里的石头向一边扔了出去 ,然后 跳向了另一边 。杰哥被这一举动吓得拔腿就往山下跑去,边跑边喊道: 阿伟死了 !当杰哥跑下山时,却看到阿伟安然无恙的在山脚下站着,以为是撞见了鬼,当场吓个半死。阿伟成功地完成了恶作剧( 本故事纯属虚构,切勿模仿 )。
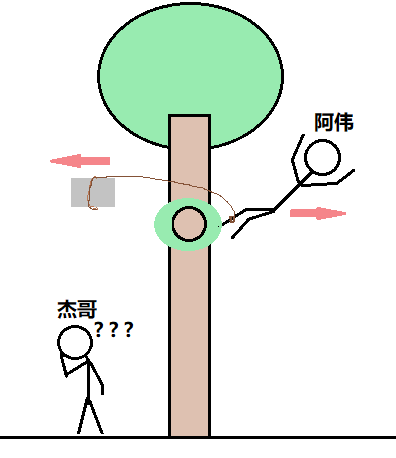
坠崖前侧视图
事实上,阿伟在这个恶作剧中分别使用了: 稀里糊涂突然坠崖计 , 拉格朗日方程计 , 绞盘自锁计 。
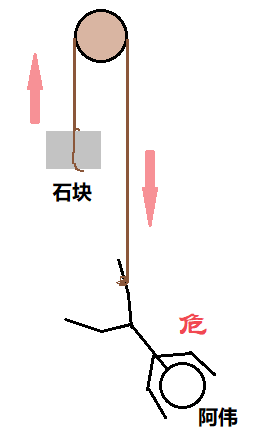
石块无法拉住人
阿伟在恶作剧前做了这样的分析,通常来讲,当石块的重量比人的重量小时,单纯悬挂着的石块是无法拉住人的,人必然会下坠摔死。但是,阿伟在下坠前,将石块扔了出去,这使 初始条件发生了变化 ,进而带来了一些奇妙的变化。
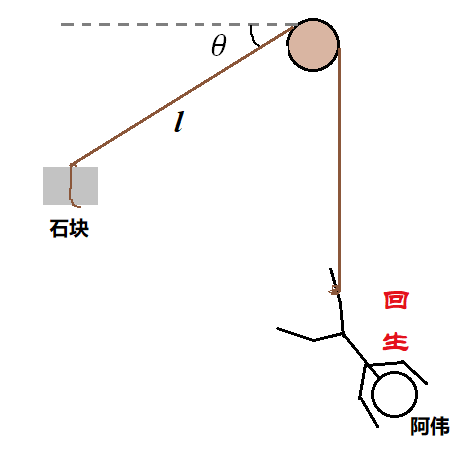
分析图
假设石块的质量是 m ,阿伟的质量是 M ,树枝相当于是一根固定的杆,为了简化问题,暂时 不考虑绳子与树枝的之间的摩擦 。如上图,系统的广义坐标只有绳子与 水平方向的夹角 和 绳子的长度 两个。因此,可以列出这样的拉格朗日方程:
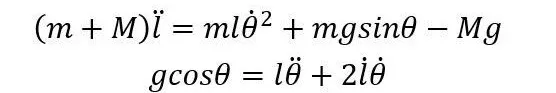
求解拉格朗日方程可以得到 石块的位置随时间的变化关系 。由于这个方程比较复杂,所以,我们直接带入初始条件(初始时绳子与水平方向的夹角为0)进行 数值求解 。从数值求解的结果可以看出,当阿伟下坠时, 石块会带着绳子绕树枝转圈圈 。
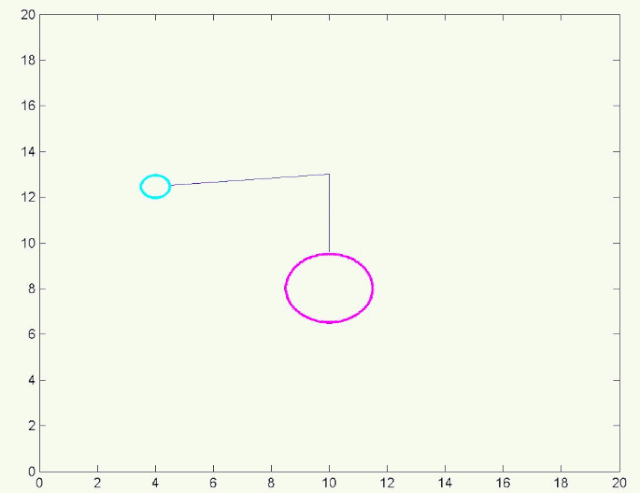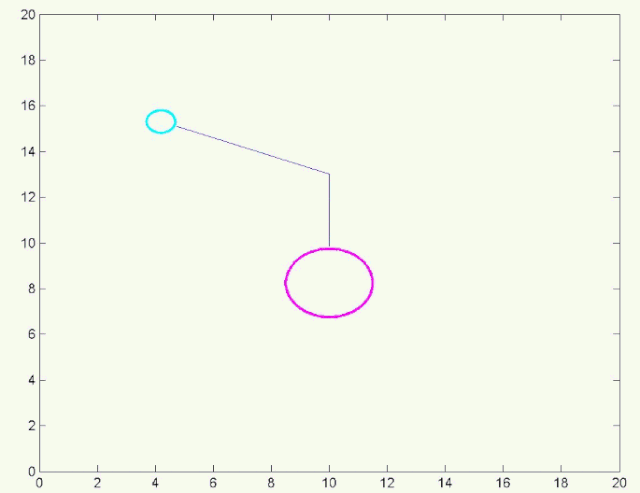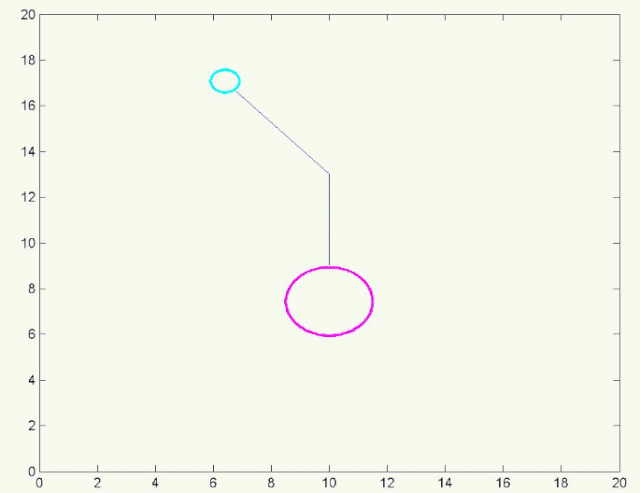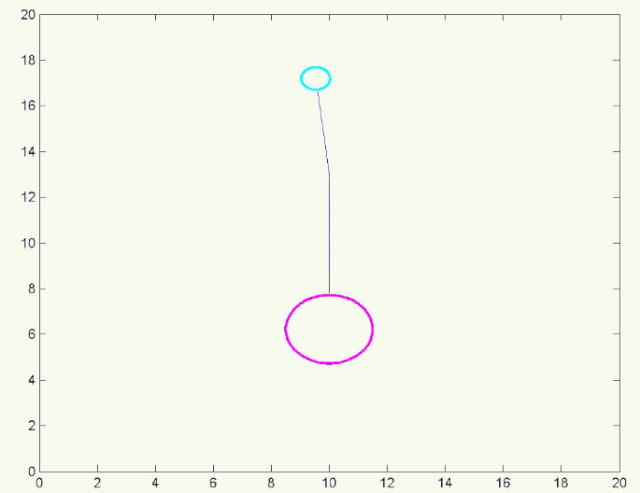
数值计算结果
当绕的圈数增加时,树枝就变成了一个 绞盘 。我们都知道,水手运用绞盘,可以用将很重的锚收起。这是因为 绞盘借助摩擦力能够将一个很小的力转化为一个很大的力 。

绞盘
根据 绞盘方程 ( Capstan equation ),当绳子绕了很多圈后,石块借助绞盘会给阿伟提供了一个很大的拉力,进而形成自锁,这使得阿伟能够在落地前停下来,避免摔伤。
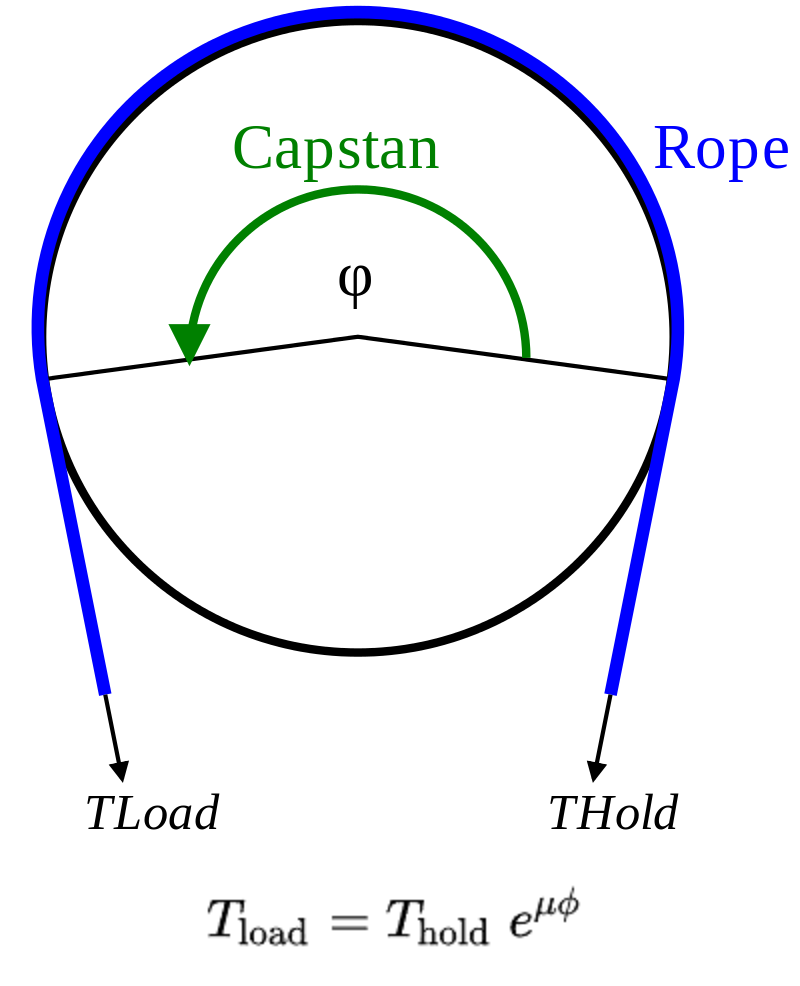
绞盘方程[5]
我们也可以用绳子一端绑着杯子,一端绑着螺母,做一个类似的小实验,可以看到,杯子在落地前能稳稳地停住。

这就是阿伟的恶作剧成功的秘密,满满的都是物理。所以说, 学好物理 , 在恶作剧这块一定能拿捏的死死的 。

总结
本文通过建模分析,运用 博弈论 , 卷积神经网络 以及 理论力学 ,分别就是什么、为什么、怎么办,深入地分析了 恶作剧出现的必然性 , 恶作剧成功的原因 ,同时也阐明了 物理知识在恶作剧中的重要作用 ,有着深远的启发意义。
“初读不识文中意,再读已成文中人。”一出出恶作剧即将上演,你准备好入戏了吗?

本研究在“老工具人了”基金的支持下完成。
参考文献:
[1] Fudenberg, D., & Tirole, J. (1991). Game theory, 1991. Cambridge, Massachusetts , 393 (12), 80.
[2] 舒幼生. 力学[M]. 北京:北京大学出版社, 2005.
[3] 杨维纮, & 秦敢. (2014). 力学与理论力学 . Ke xue chu ban she.
[4] 周志华. (2016). 机器学习 . Qing hua da xue chu ban she.
[5] 绞盘方程
编辑:Shiny
↓ 点击标题即可查看 ↓
1. 物理定律告诉你:表白可能巨亏,分手一定血赚
2. 震惊!昨天你们立起来的扫把,甚至真的惊动了 NASA
3. 酒精和 84 消毒液到底能不能一块用?
4. 一次性医用口罩是怎么做出来的?如何消毒?
5. 数学好玩个球啊,这支豪门球队用一群数理博士横扫球场
6. 「测温枪」到底是怎样测出你的温度的?
7. 等量 0 度水和 100 度水混合能得到 50 度水吗?
8. 人类为什么喜欢亲吻?
9. 病毒从哪里来?
10. 一见钟情,到底靠不靠谱?
